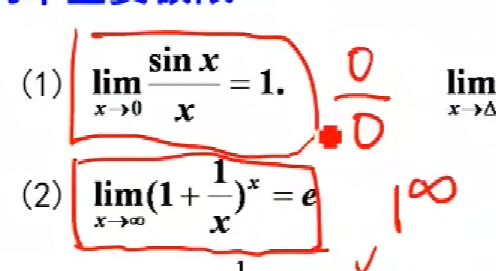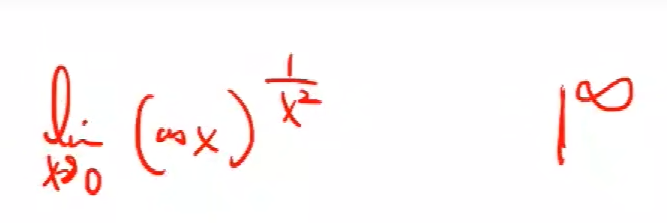一个数列有没有极限，极限存在那么极限是多少与前有限项没关系，所以并不要求从“第几项”开始。

这里原本描绘Xn和Zn的"Nx和Nz“可能不一样，没关系，取一个N比Nx和Nz都大就可以。

不能一项一项求可以想到真题

不好合的话，可以想到放缩

这里缩小是所有的分母换成最大的分母

放大所谓所有的分母换成最小的分母

并运用夹逼原理

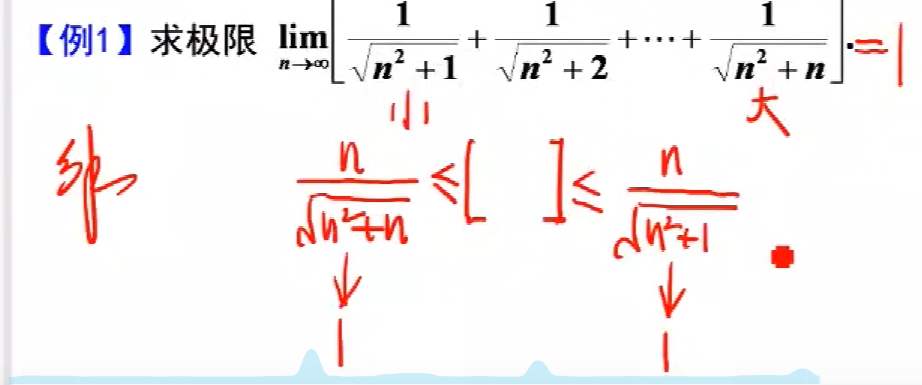
函数也有夹逼原理

自变量趋向x0或者无穷都可以

这题启示求某个会振荡的函数的极限可以用夹逼原理。

补充一个扇形面积

需要熟悉的一个结论：

补充二倍角公式:

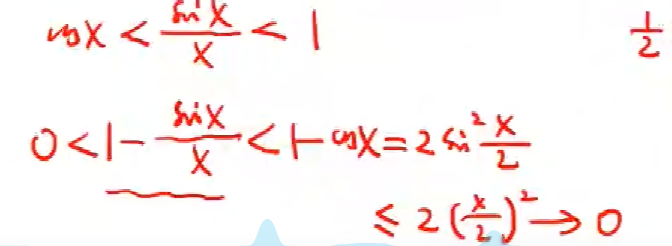
注意，这个小于等于

是从蓝色框里面出来的

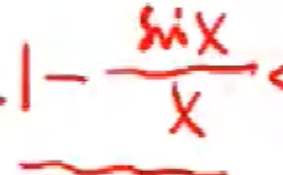
到这里，这个式子两边都趋向于零

它又是被1减的

换成它减去一，那么就恰恰证明了它的极限是一

但是这只是右极限，因为这个是从x在0到二分之Π里面出来的。

但是这！是个偶函数!所以证出来它的右极限等于1之后，对称一下，左极限也等于1了。

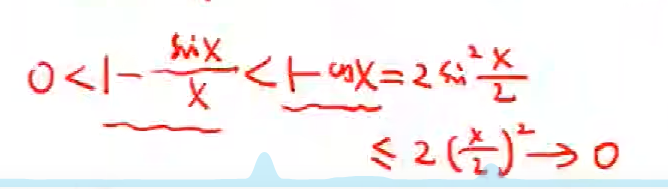
同时这里还正好证明了1-cosx趋向于0点的时候，极限为1。

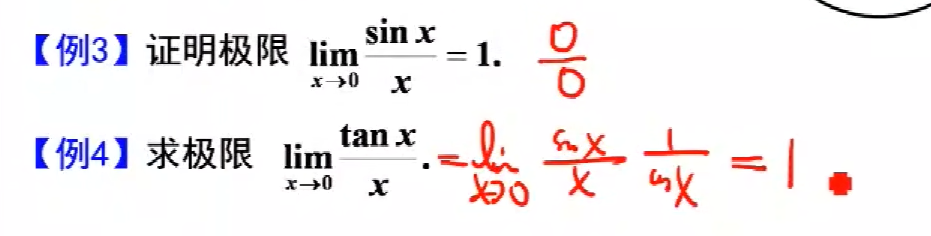
这里例4就是用已知的0比0，求出未知的0比0

这个也是。

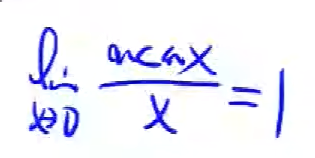
”第一项就是上界“”第一项就是下界“

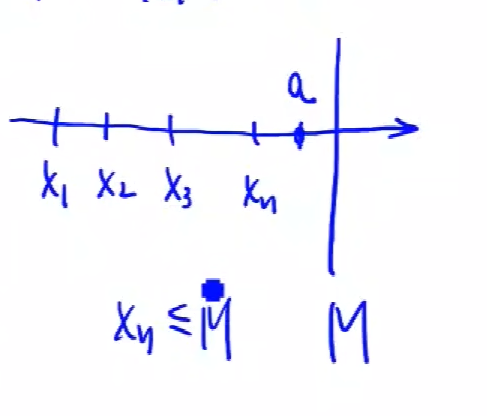
从几何上看，就是一直在接近于一个数。

补充这个，中学时期的不等式。

关键在于又乘了个1

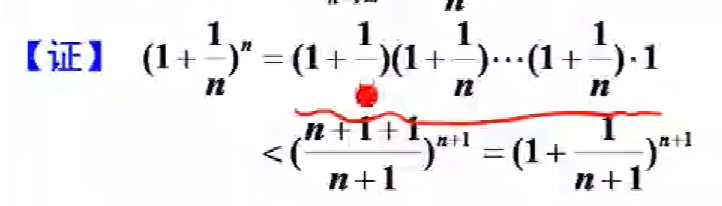
由此可以证明出单调。

注意这个乘以1，主要是针对于，不等式的，这个1不符合数列，但是可以当作成员，使用在不等式当中。

这里求有界更加证明了，使用这个”加上去相乘的时候“并不要求你构造的项属于数列。

单调递增，上有界，那么这个极限就存在，极限存在，那么这个极限就是个实数。

这个就是e，e是个记号，最后反过来求这个e的时候，就得到后来的无理数。

函数也有单调有界准则，但是用得比较少。

这里为了使得数列的结论能够运用在函数，运用到取整函数，这是因为，数列的n的取值是离散的，而x的取值是连续的。

并且使用了放缩，这里证明了正无穷趋向于e（其实应该也就是夹逼)。

新问题转换成老问题

倒代换

夹逼多用于n项he

单调有界多用于递推关系定义的数列极限

两个重要极限可以一般化

但是注意”不能等于0“