自然定义域:
数学术语,是对抽象地用算式表达的函数,通常约定这种函数的定义域是使得算式有意义的一切实数组成的集合。
集合怎么表示?:
1. 列举法:逐一列举出集合中的元素,写在大括号内,例如集合{红,绿,蓝}表示三原色的集合。
2. 描述法:通过描述集合中元素的共同特征来表示集合,格式为{x|P(x)},如集合由2的平方根组成可以表示为{ x | x^2 = 2 }。
3. 图示法:利用二维平面上的点集表示集合的方法,如用矩形或圆形表示集合,是集合的一种直观的图形表示法。
4. 符号法:使用特定符号表示集合,如N表示非负整数集合,Z表示整数集合。
不同的描述法还需注意以下几点:
- 描述法中,符号左侧元素的所属范围在实数集时可以省略不写。
- 描述法的代表元素和描述条件要写在大括号内,避免误解。
在集合论中,集合元素具有确定性、无序性和互异性的特性,而元素与集合间存在属于和不属于的关系。集合的基本结论包括集合是其自身的子集、子集关系的传递性以及集合的并集、交集等运算规律。集合表示方法的选择取决于具体情况,不同的方法有利于不同类型集合的描述与表达。
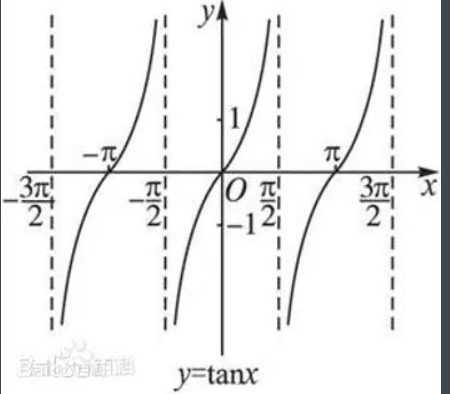
正切函数:
正切函数tan(x)的定义域是{x | x ≠ (π/2) + kπ, k ∈ Z}。
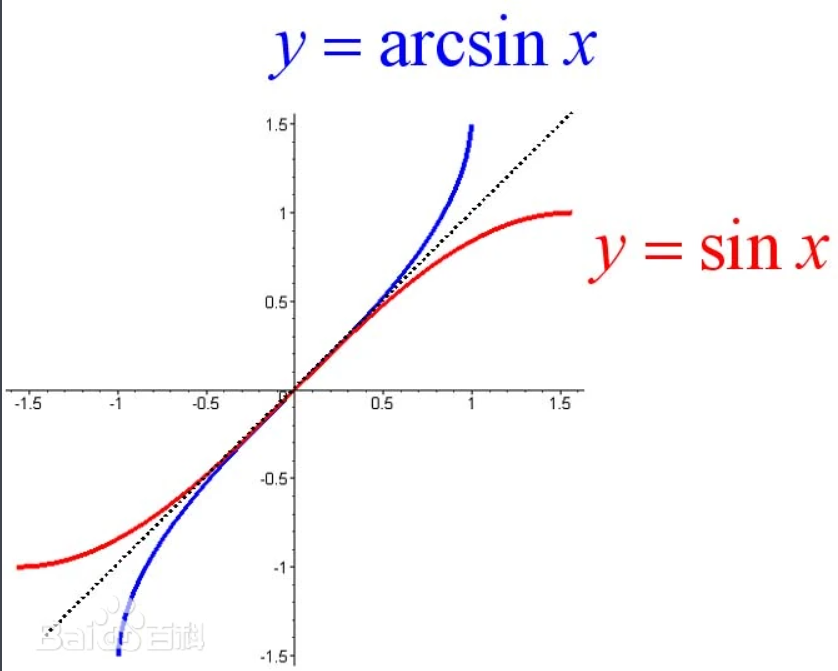
反正弦函数:

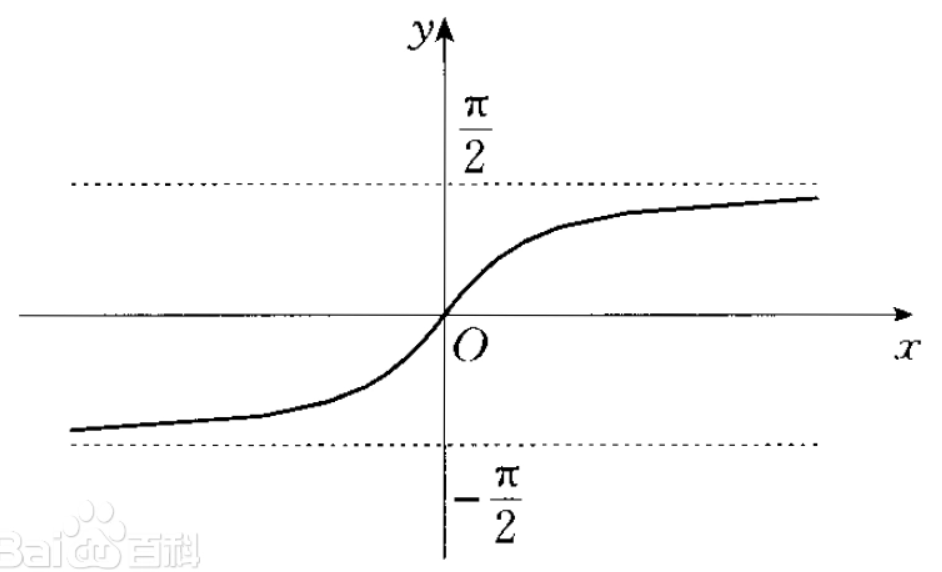
反正切函数:

自然对数:
自然对数是以常数e为底数的对数,记作lnN(N>0)。在物理学,生物学等自然科学中有重要的意义,一般表示方法为lnx。数学中也常见以logx表示自然对数。
对数函数:




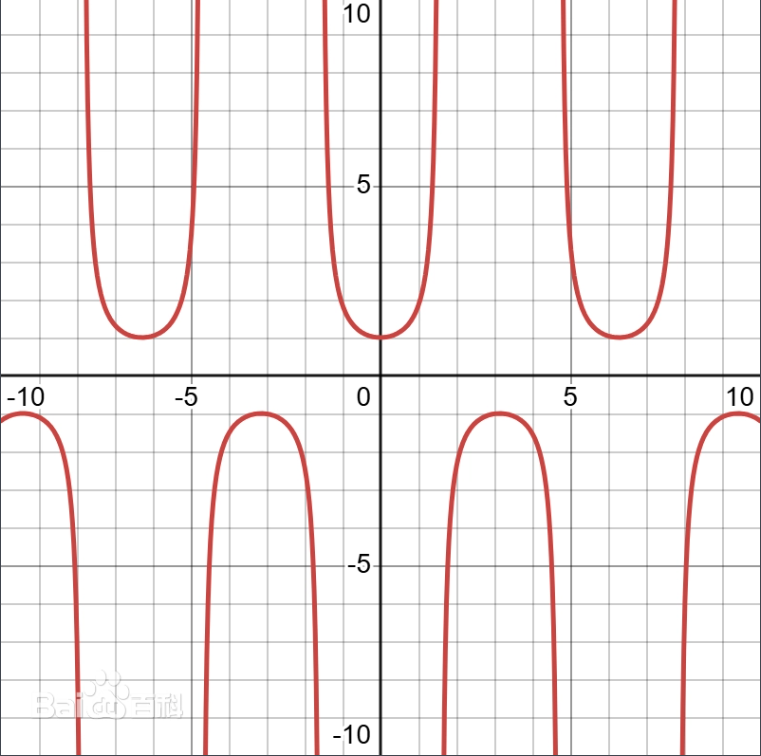
正割函数: