想来居然漏掉了一节课。
在今天之前，我对学习越来越应付。
今天发现，没有比要应付，应付与不应付，感觉上也是一样的。
还是好好学吧。
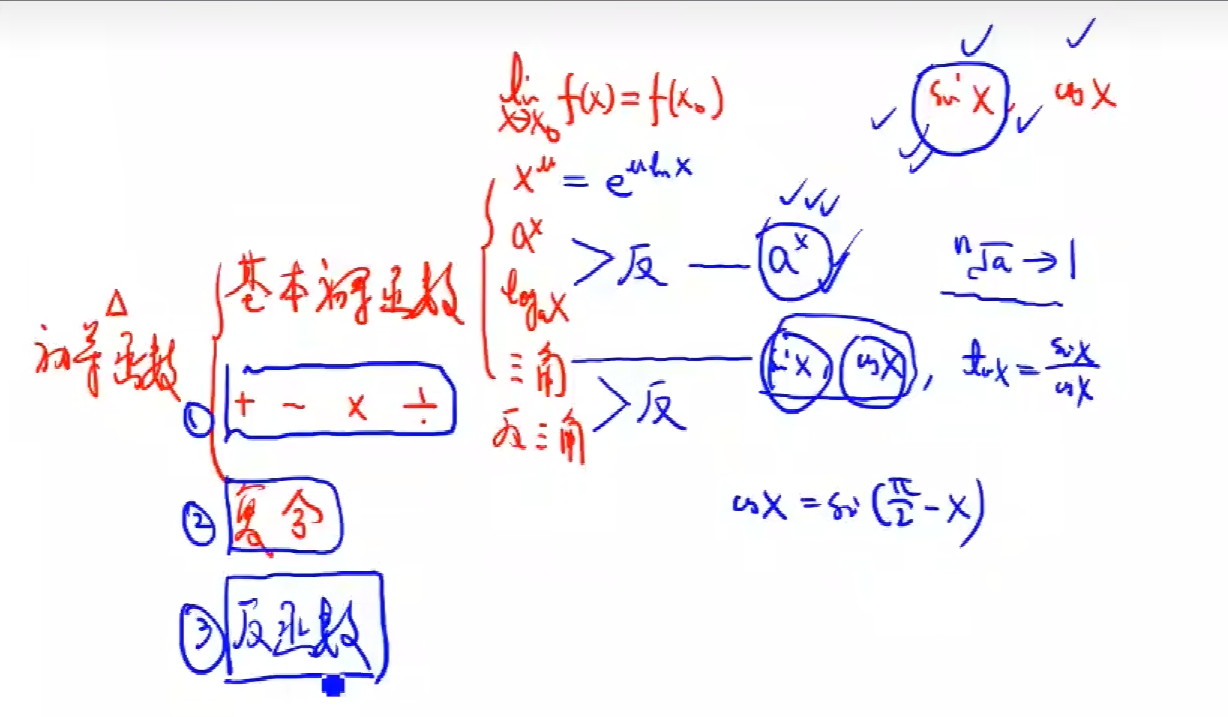
老师的思路是，把庞大的问题化解为小问题，小问题中抓住关键问题，就可以解决庞大的问题。
像这里sinx可以用定义解决。（在7.文章中已经解决了，然后cosx也可以用类似的问题解决，然后tanx就是sinx除以cosx的商。）
然后幂函数可以转化为带对数的指数函数，指数函数是对数函数的反函数。那么就解决ax的问题就可以。a开二次方趋向于1可以解决ax的问题。
这样基本初等函数如果在解决了复合函数与反函数以及和差积商的连续性问题上。
再解决sinx cosx ax就可以了。
假设现在已经解决了ax的问题。
接下来讨论的就是如何解决复合函数与反函数以及和差积商的连续性问题。
老师这里展现了另一个思路就是，上下同时乘以“1”。
利用等价无穷小来算。
归纳出的比较简单且方便的方法来做
其实这题为什么只讨论间断点呢？其实就是用到了前面讨论的各种初等函数的连续性，不然是怎么知道其他地方都连续呢？
不过这个本身不是一个初等函数，因为它不好用一个解析式表示。
作业感受：
记录一题没写出来的
或者说我这么处理本身本质上就还是加减关系。应该更加有可能是这个原因，而不是说分子分母的使用“等价代换”的次数一样。我觉得更有可能是因为这个原因。
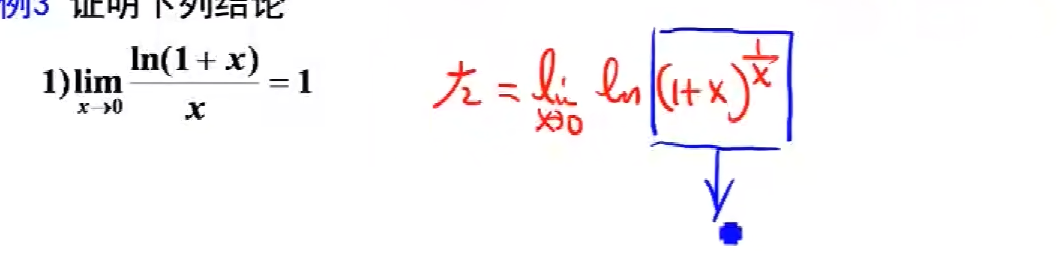就是把1/x当成ln前面的系数，然后系数又转成指数
越来越感觉做题就是混眼熟，像这题，还得记得这几个特例。唉